1 对Sklearn中Decision Tree的简单理解
在Sklearn中Decision Tree分为两个类型(基于CART),一个是基于类型的分类器,另一个则是针对连续型变量的回归模型。
分类树在我个人看来是属于有监督的机器学习的一种,对于特征的输入,都有一个确定的分类来对应这些特征。比如年龄在0-17岁之间的人都可以定义为未成年,18-65岁之间的可以定义为劳动人口,而66岁及以上的则可以定义为退休老人,这就是一种典型的分类树。分类树的模型训练着重于让机器自动学会在复杂情况下的分类方法,这里人类首先为所有的数据打上标签,而机器主动学习背后为不同数据打标签的规则,从而在应用层面上之后会自动为新的数据打标签。分类树并不在本文的学习范围内,因此不再赘述。
回归树同样是有监督的学习,但它的目的并不在于为数据打标签,而是更精确的预测一个输入所对应的输出。这个输出值并不是几个类别,而是精确的预测值。因此,回归树的训练集应该是连续型变量,它的训练方式应当如同建立回归方程一样去理解,但它可以做到回归方程难以做到的对异常值的妥善处理。通常当数据中存在异常值时,回归方程倾向于忽略异常值,但同样的会造成拟合度下降。回归方程或者可以通过升维等方式来囊括进异常值,但这就会造成回归方程在异常值附近的拟合十分怪异(升维会造成曲线在异常值附近有非常夸张的变化),也同样对附近正常值的预测造成了影响。
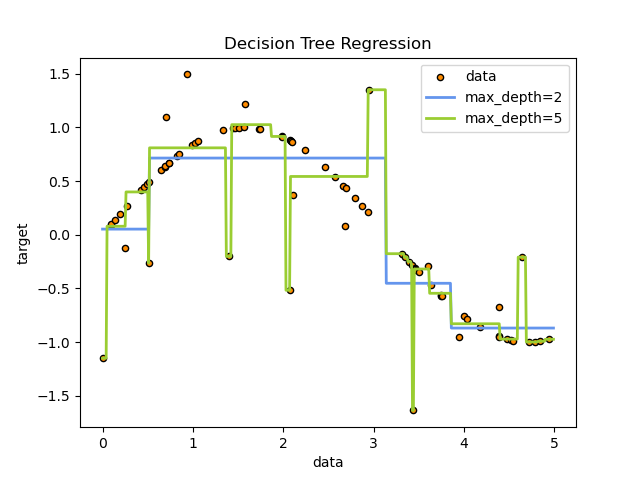
回归树则用另一种思路解决了对异常值的处理问题。它将输入数据做了极其细碎的切割(切割程度取决于对模型参数的规定),对每一个小的数据分类都有一个精确的预测值,因此可以特地为异常值建立一个子类,从而把它囊括进去的同时不影响对临近正常值的预测(因为异常值与正常值属于不同的子类中)。然而这样的缺点也显而易见,即如果将回归树模型切的过于细碎,那模型对于输入的扰动会极度敏感,从而造成过拟合,失去了对数据整体分布的合理判断(上图)。
然而回归树依然适用于相当多的复杂场景来作为有效的预测手段。这里的原因我理解的是因为对于异常值的定义。数据的收集中不可避免的会遇到奇怪特点的值,但是对于这样的奇特数据笼统的归纳为异常值并不合理。在现实环境中收集的数据在条件受限情况下或数据量有限的情况下可能是分布不均的,这样分布不均的数据中出现几个不符合整体分布情况的点有两种可能。首先,它可能是真的异常值,非常罕见的受到了观测外因素的扰动出现不正常现象,这可以归纳为自变量的不完整或者是超出理解范畴的变化或是观测过程出现错误。其次,它可能只是在正常分布范围内但是类似数据收集的过少,从而给人一种异常的感觉,但是它事实上仍然是正常值。那么此时抛弃这个值是对模型完整性的损害。总的来看,真实数据(非仿真数据)出现真正异常的可能性并不大(即存在超出理解的因素扰动了结果)。在真实数据可信性较高的情况下,抛弃一些分布“不合理”的值会事实上降低模型对这种情况的拟合度,因此考虑到两种情况的平衡,囊括进“异常值”是更合理的选择。但是这些异常值会为回归方程等线性、非线性拟合造成困难,而这个困难恰恰可以被决策树的特点所消解。因此,总的而言回归树在数据结构和数据分布相对复杂和难以理解的情况下是一种快刀斩乱麻的有效手段。
Random Forest Regressor是Decision Tree Regressor的更极致改进
2 Sklearn中回归树的评价指标
2.1 4个在Sklearn中内置的评价指标
Sklearn 1.2.1版本中内置了4个criterion,也可以称为损失函数,来衡量分类效果,分别是“squared_error”, “friedman_mse”, “absolute_error”, “poisson”。这里的损失函数的功能与在ANN中是一致的,即衡量按即有分类情况下模型的预测值与真实值的差距,从而在下一次调整分类标准向降低误差值的方向靠近直至达到模型参数的设定。
2.2 squared_error
这里的squared_error在我阅读了Sklearn的文档后认为就是MSE(Mean Squared Error)均方误差,也称L2损失(MSE在Sklearn中对Decision Tree的Regression criteria中做了解释,并清楚的在DecisionTreeRegressor函数中明确说明了squared_error就是MSE)。
\[MSE(y_i,f_i)={\sum^{N}_{i=1}{(y_i-f_i)^2} \over n}\]$f_i$是模型的预测值,$y_i$是真实值,n是样本总数。
在回归树中MSE为左右两支子树的MSE之和,算法通过计算得到最低的MSE来确定左右两支子树的分类界限在哪里。
\[MSE = {MSE_{left} \over weight_{left}} + {MSE_{right} \over weight_{right}}\]虽然MSE的计算十分简单易懂,但在squared_error中模型对于不同程度的误差关注度是不一样的,这是需要在使用中注意的。MSE的计算方式天然决定了它对小于1的误差十分宽容,甚至进一步减弱了小误差对模型的影响,但对大于1的误差则进行了平方的放大。因此,就需要慎重考虑输入参数中是否存在极小的值,或者是否对数据做归一化(需要强调的是在决策树中没有必要进行归一化,因为模型对数据的量纲不敏感)。总而言之,squared_error是一种对大误差有更大惩罚的函数,而对小的误差不敏感。
2.3 friedman_mse
friedman_mse是基于MSE这种思路的一种改进,但计算方法完全不同。MSE从数据分布的角度来降低模型预测的误差,而friedman_mse则考虑了事件发生的概率来修正分类标准。
原版Friedman的方程中为如下定义:
\[i^2(R_{l},R_{r})={w_lw_r \over w_l+w_r}(\bar{y_l}+\bar{y_r})^2\]$w$是子类的权重,$\bar{y}$是对应子类的平均值
在Sklearn中,模型使用如下方程计算:
\[Sum_{left}=\sum^{N}_{i=1}{y_{left}}\] \[Sum_{right}=\sum^{N}_{i=1}{y_{right}}\] \[diff=w_r*Sum_{left}+w_l*Sum_{right}\] \[proxy\ impurity\ improvement={diff^2 \over w_r*w_l}\]$w_r$和$w_l$是子树的权重,$Sum_{left}$和$Sum_{right}$是对应子树内真实值的总和
在friedman_mse中预测值并不重要,它侧重的是对真实值概率分布的最佳分类。这里它用了数学期望而不是平均值来做$diff$的计算,并目标向$proxy\ impurity\ improvement$的最小化。因此,当数据的分布相对不符合简单的曲线,但存在明显的概率分布特征时,可以使用该函数做回归树的标准。
2.4 absolute_error
absolute_error就是MAE(Mean Absolute Error),也称L1损失。这个函数中规中矩,在回归树中目的同MSE一样,在程序设定条件下,最小化L1损失。
\[MAE={\sum^{N}_{i=1}{|y_i-f_i|} \over n}\]$f_i$是模型的预测值,$y_i$是真实值,n是样本总数。
2.5 poisson
poisson在该程序中是指Half Poisson deviance。该函数同样也是基于概率分布来拟合模型,只不过是基于泊松分布。既然是泊松分布那对于该标准的使用就有一定的限制。该损失函数可以理解为用于预测某时间段访客的多少,或者某限定条件下多少人或物出现在某地。基于这种适用条件,首先该函数仅适用于因变量大于0的数据,因为事情的发生要么是不发生要么就是发生了,但不会有负的情况;其次该函数适用于因变量为整数的数据集,因为限定条件下,人或物出现的数量都是整数的,比如5个人,6只鸟等。另外,在sklearn中同样也指出了该函数的运行显著慢于MSE,因此在对大数据进行机器学习时需要平衡其中的时间与能源成本。
\[Poisson\ deviance = {2\sum^{N}_{i=1}{(y_i\log{y_i \over f_i} + f_i - y_i)} \over n}\]$f_i$是模型的预测值,$y_i$是真实值,n是样本总数。
3 Sklearn模型中返回的Score是什么
在Sklearn中训练的回归树模型中可以输出模型的Score,Score反映了模型对数据集的拟合程度,在这里对Score做一定的解释。
Sklearn中的Score是基于$R^2$(不同于MSE)。$R^2$的计算非常简单,仅计算预测值与真实值的误差的平方和以及真实值与真实值的平均值的差的平方和,并做简单的除法和减法计算。
\[u=\sum^{N}_{i=1}{(f_i-y_i)^2}\] \[v=\sum^{N}_{i=1}{(y_i-\hat{y})^2}\] \[R^2=1-{u\over v}\]$f_i$是模型的预测值,$y_i$是真实值,$\hat{y}$是真实值的平均。
在这个计算中,比较的是模型的预测结果的残差平方和以及模型的总平方和的差距。在这里对确定的数据集而言很明显$v$是固定值,而当预测值与真实值偏差过大时$u$会增大从而使$u\over v$增大,当误差超过了模型的平方和时$R^2$会出现负值,而当预测结果十分靠近真实值时$u\over v$趋近于0,即$R^2$接近1。因此,总结来说$R^2$是集合$(-\infty,1]$中的一个数,且越靠近1则表明拟合效果越好。
Tips: 在Sklearn的回归树中$f_i$是子树内所有因变量的平均值,即$f_i=\hat{y}$(对应叶子)
免责:该博客及博客内容均为作者个人见解,未经严谨的学术论证,所以并不对内容的正确性做担保。如有讨论欢迎通过邮件的方式进行沟通,我会积极学习并修改错误 :D